HOLA, BIENVENIDOS!
Aquí podrás afianzar tus conocimientos en matemáticas y sus ramas estadística y geometría.
Sigue las instrucciones que te permitirán avanzar, utilizando adecuadamente y de manera consciente el material proporcionado como vídeos, textos y diferentes actividades que te ayudaran a demostrar lo aprendido y a afianzar tus conocimientos.
PRUEBA DE DESEMPEÑO DEL PRIMER PERIODO.
https://forms.gle/DmHHn98XbtKS6EK46
PRUEBA DE DESEMPEÑO DEL PRIMER PERIODO.
https://forms.gle/DmHHn98XbtKS6EK46
Es así como iniciaremos con matemáticas (aritmética).
DESIGUALDADES E INECUACIONES EN LOS NÚMEROS REALES
DESIGUALDADES E INECUACIONES EN LOS NÚMEROS REALES
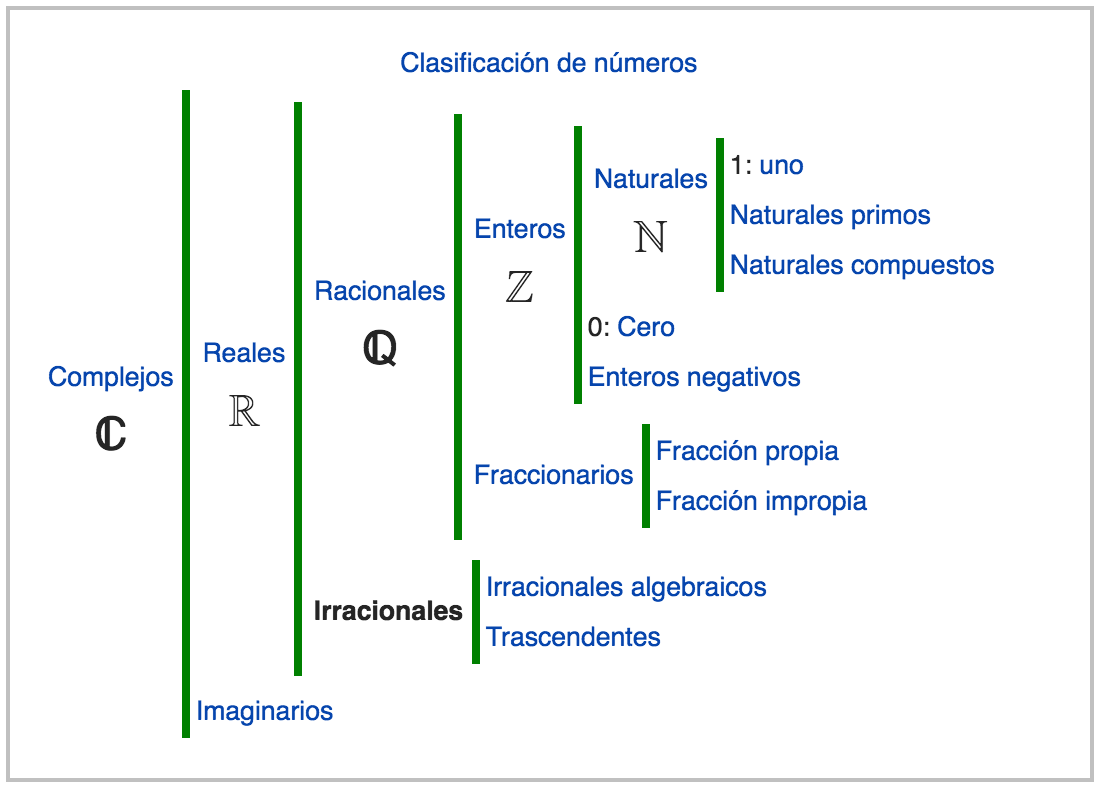
Iniciemos recordando que son NÚMEROS REALES.
Los números reales son todos los números que pueden ser representados en una recta numérica, el conjunto de los números reales se denotado por . Como conjunto, los números reales contiene a los siguientes subconjuntos:
Desigualdad: Es una relación de orden que se da entre dos valores cuando éstos son distintos (en caso de ser iguales, lo que se tiene es una igualdad), conectadas a través de los signos: desigual que ≠, mayor que >, menor que <, menor o igual que ≤, así como mayor o igual que ≥, resultando ambas expresiones de valores distintos.
Inecuación: Es una desigualdad entre dos expresiones algebraicas en la cual los conjuntos (miembros) se encuentran relacionados por los signos (menor que), (menor o igual que), (mayor que) y (mayor o igual que). Por ejemplo:
o
Estas expresiones algebraicas son inecuaciones siempre y cuando las variables tomen valores que satisfagan la desigualdad.
Observa el siguiente vídeo que te hablara de las propiedades básicas de la desigualdades, toma nota de estas para así realizar la actividad indicada.
PROPONGO un ejemplo para cada propiedad y trata de gratificarlo como consideras que quedaría.
CLASES DE INTERVALOS
Ahora veremos como representar un intervalo
Ejercicios de intervalos
1.- Escribe en todas las formas posibles los siguientes intervalos y semirrectas:
a) { x / –2 ≤ x < 3}
b) Números mayores que –1
c) (–∞, –5]
d) Números mayores o iguales que –7 y menores que 19.
e) Números mayores que 9 y menores que 5.
2.- Completa la siguiente tabla.
3.- Representa los intervalos en la recta real y exprésalos como inecuaciones:
A = [–4, 1]
B = [–1, 4)
C = (2, +∞)
5.- Representa los intervalos en la recta real y exprésalos como inecuaciones:
A = (–∞, 2]
B = [1, 5]
C = (2, 4]
http://mimosa.pntic.mec.es/jgomez53/docencia/eso4-ejercicios%20de%20intervalos.pdf
Ahora, es tiempo de practicar
VAMOS A GEOMETRÍA
¿Conoces los diferentes tipos de triángulos?
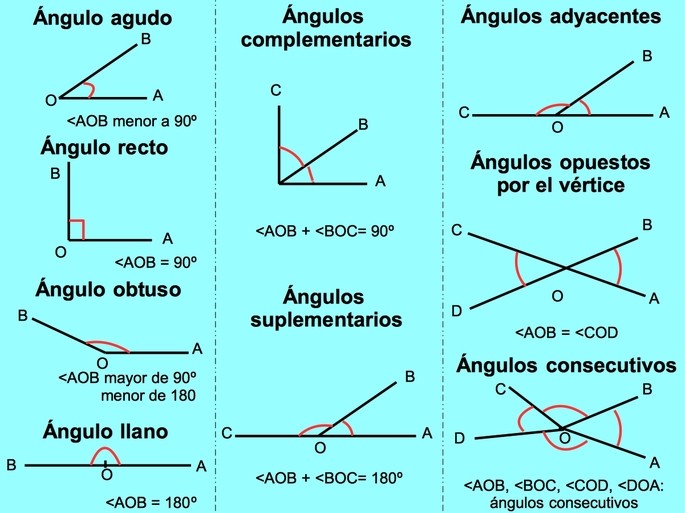
Clasificación de ángulos y triángulos
Identifica cada tipo de triangulo según sus ángulos.
a. un triangulo con ángulos que miden 60 grados recibe el nombre de ___________ .
b. un triangulo con angulo de 90 grados recibe el nombre de ________________.
c. un triangulo con un ángulo de 120 grados recibe el nombre de ____________.
EJERCICIOS DE ÁNGULOS
VAMOS A
Elabora un problema estadístico con los
pasos indicados en clase y representa su información en dos clases de gráficas
diferentes, explica.
REFERENCIAS
https://www.ck12.org/book/ck-12-conceptos-de-matematicas-de-la-escuela-secundaria-grado-6-en-espanol/section/9.7/
Matemáticas (aritmética).
Matemáticas (aritmética).
OPERACIONES
CON INTERVALOS
Dado que los intervalos constituyen un tipo particular de conjuntos,
definiremos a continuación algunas operaciones, con conjuntos en general, e
ilustraremos estas operaciones mediante ejemplos, de entre los cuales en
algunos casos se involucraron intervalos.
INTERSECCION
Sean A y B conjuntos. Se define la intersección de A y
B y se denota A ∩ B, al conjunto cuyos elementos
pertenecen a A y también a B.
Simbólicamente se tiene que:
UNION
Sean A y B y conjuntos. Se define la unión de A
y B y se denota A U B, al conjunto cuyos elementos pertenecen al menos a
uno de los dos conjuntos A y B.
DIFERENCIA
Sean A y B conjuntos. Se
define la diferencia de A y B y se denota A ─ B, al
conjunto cuyos elementos pertenecen al A y no a B.
1. Dados los siguientes conjuntos:
HALLAR:
VAMOS A GEOMETRÍA
ACTIVIDAD 2
En compañía de tu familia y utilizando un material
adecuado, realiza tres de las figuras anteriores y halla su área y volumen según
las medidas que utilices.












No hay comentarios.:
Publicar un comentario